Alongside wealth inequality, math talent inequality is one of the most brutal forms of inequality on this planet. Like wealth inequality, it is brutal at every step of the ladder.
It’s like fractals. The 1% is insanely stronger than the 99%. The 0.1% is yet again insanely stronger. And yet again the 0.01%. The 0.0001% is a whole different species. I have friends in the 0.000001% and they scare the hell out of me. And then there’s Terry Tao.
When Usain Bolt set his 9.58 world record in the 100m dash, he ran 1.5% faster than the silver medalist, and only 3% faster than the last-place finisher. Math talent inequality feels radically different from that.
When I discussed the issue with Hugo Duminil-Copin, the 2022 Fields medalist, he shared his perception that Terry Tao is at least 10x faster than he is when it comes to processing new mathematical concepts and making sense of them.
Hugo’s view is far from marginal. In fact, most career mathematicians that I know have similar perceptions of the talent gap.
Like all creative endeavors, mathematical research builds on passion, drive, luck, and the willingness to venture deep into uncharted territory. Yet it does place cruel and unusual demands on the brain, and some people do seem to possess a “natural” advantage.
How do you explain John von Neumann who, at age six, could divide eight-digit numbers in his head?
How do you explain Gauss, born to poor and illiterate parents, who proved at age 19 that regular heptagons aren’t constructible with compass and straightedge, a problem that had resisted the smartest people for two millennia?
How do you explain Terry Tao? How do you explain Ramanujan? How do you explain Galois? How do you explain Grothendieck?
How do you explain, on the other hand, the millions of kids who struggle with elementary math?
To anyone who has engaged with advanced mathematics, or to anyone familiar with its history, it is obvious that social determinism can only explain a fraction of what is actually taking place. This is why so many people instinctively default to the opposite explanation: innate ability.
Yet, as we’ll see, the jarring magnitude of math talent inequality is a compelling evidence against genetic determinism.
The uncalibrated world of genius
Before going any further, I should clarify the scope and semantics of my assertion.
I am obviously NOT claiming that genes play no role in this story, as there is massive scientific evidence of the contrary. Human cognition emerges from the human brain, a physical organ whose capabilities are clearly affected by genetic variability. There are known genetic conditions that cause severe learning disabilities and this is just the extreme end of a spectrum.
My point is that genetics alone cannot “explain” genius, at least not in the casual sense most people give to these words.
Wiktionary defines talent as “marked natural ability skill.” When this marked ability becomes extraordinary, we enter the territory of genius:
I am perfectly aware that these are fuzzy notions and I won’t attempt to fix this.
Neither talent nor genius are well-defined scientific concepts, yet they are pragmatic constructs that capture an essential feature of our daily experience: it does feel that “intelligence” and “creativity”—whatever these words mean—are distributed in a markedly uneven manner, and that a few people are quite extraordinarily endowed.
I ran a quick unscientific experiment on how my audience perceives the intelligence gap:
Please give your gut-feel answer, without thinking too much: compared to a “normal person”, how much smarter was Einstein?
Out of 585 votes, 14.5% went to “20x smarter”, and a full 25% of respondents selected the top option, “on a different planet”.1
This framing is ridiculously over-simplistic, as there is no calibrated scale of intelligence that adequately captures the uniqueness of people like Einstein. IQ, which was designed as a low-cost instrument for spotting learning disabilities, is notoriously uncalibrated at the top.
Yet, as we saw with the example of Hugo and Terry, there are indirect ways of probing the magnitude of the talent gap, and they do point toward massive differences. In math and related domains, genius does feel like extreme wealth, with a distribution that resembles a Pareto distribution.
This is the phenomenon we call genius. In our experience, the cognitive talent gap feels monstrous, abysmal, orders of magnitude wider than typical within-species variability.
Mathematical genius is especially striking as it often manifests itself from an early age, outside of any obvious social explanatory pattern. I completely get why most people would presume that it is innate—I used to think that way too.
This is the heuristic behind the genius myth: faced with extraordinary talent, people look for an extraordinary explanation, and the only one they can think of is extraordinary genetics.
This heuristic is at play in Hans Bethe’s famous characterization of John von Neumann (Bethe was the 1967 physics Nobel prize laureate, and he had worked alongside von Neumann on the Manhattan project):
I always thought von Neumann’s brain indicated that he was from another species, an evolution beyond man.
Yet this heuristic is mathematically wrong: when you are faced with Pareto-like, species-redefining inequalities, the correct heuristic is to assume that they are NOT primarily caused by genetic variability.
While genetic variability is certainly a contributor to cognitive inequality, it cannot be the primary driver of the genius phenomenon, at least not in the near-deterministic manner envisioned by Bethe.
The Gaussian world of polygenic heritability
The correct framework for analyzing these heuristics is the notion of heritability, a statistical measure of the fraction of the variance of a trait that is associated with genetic variability.
Real-world genetics never quite follows the textbook pattern of Mendelian genetics, where one single gene deterministically controls a specific trait. Even eye color, often presented as a prototypal example, is influenced by a multiplicity of genes.
If there was a “math gene”, a single gene with a paramount influence on math talent, it would have been located decades ago.
In fact, the norm is rather the opposite: all high-level human traits exhibit a certain degree of heritability, but they are almost always highly-polygenic, that is, under the influence of a great number of genes whose individual contribution is always tiny. For example, despite hundreds of studies involving millions of participants, no single genes has even been found to cause 1% or more of the population variance of any complex human behavorial trait.
Wealth is a good example of a highly polygenic trait with low heritability. While there are massive non-genetic factors influencing one’s net worth, it is also true that it helps to be smart, good-looking, and generally healthy. These factors are influenced by our entire genome, through fabulously complex pathways.
Height is the prototypical example of highly-heritable highly-polygenic trait, where genome-wide studies have identified hundreds of contributing loci and heritability is estimated to be close to 80%.
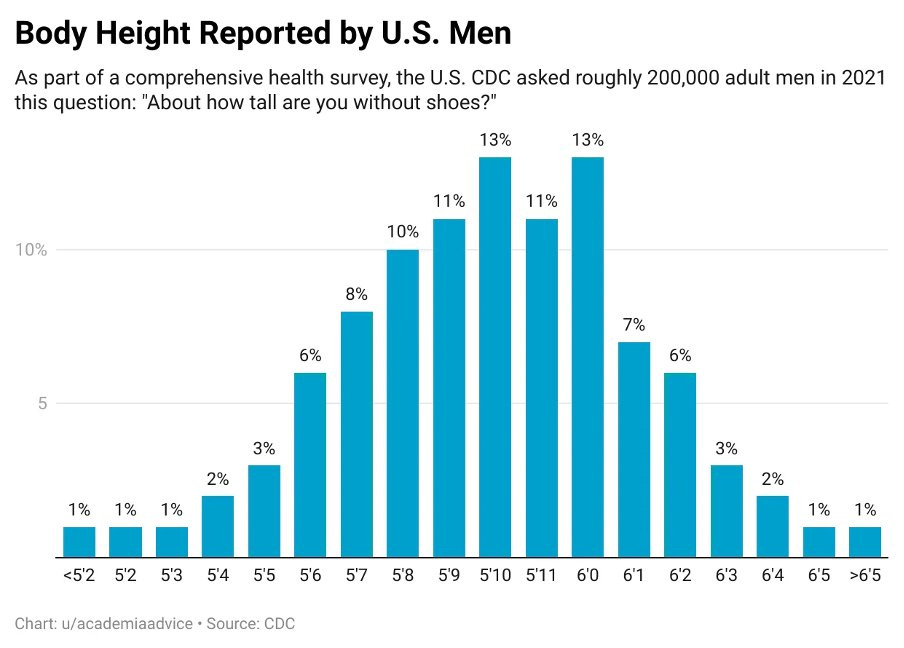
Now there’s something striking about the distribution of height: it looks like a bell curve, aka a Gaussian or a normal distribution.
In fact, the self-reported body height of US men would fit a near-perfect Gaussian if it wasn’t for the cheaters claiming to be 6’, when they’re only 5’11.
The explanation is simple. Gaussians typically occur when you model the cumulative impact of large numbers of independent coin flips, which is precisely what you’d expect to see with a highly-heritable highly-polygenic trait:
under a linear model of genome expression, the genetic contribution is obtained by adding the contributions of each individual genes, which behave like independent coin flips;
this results in a polygenic score that obeys a Gaussian law;
if the heritability is high, one would expect this Gaussian input signal to remain prevalent in the distribution of phenotypic outcomes.
Here’s a simulation of a Gaussian polygenic trait with 80% heritability:
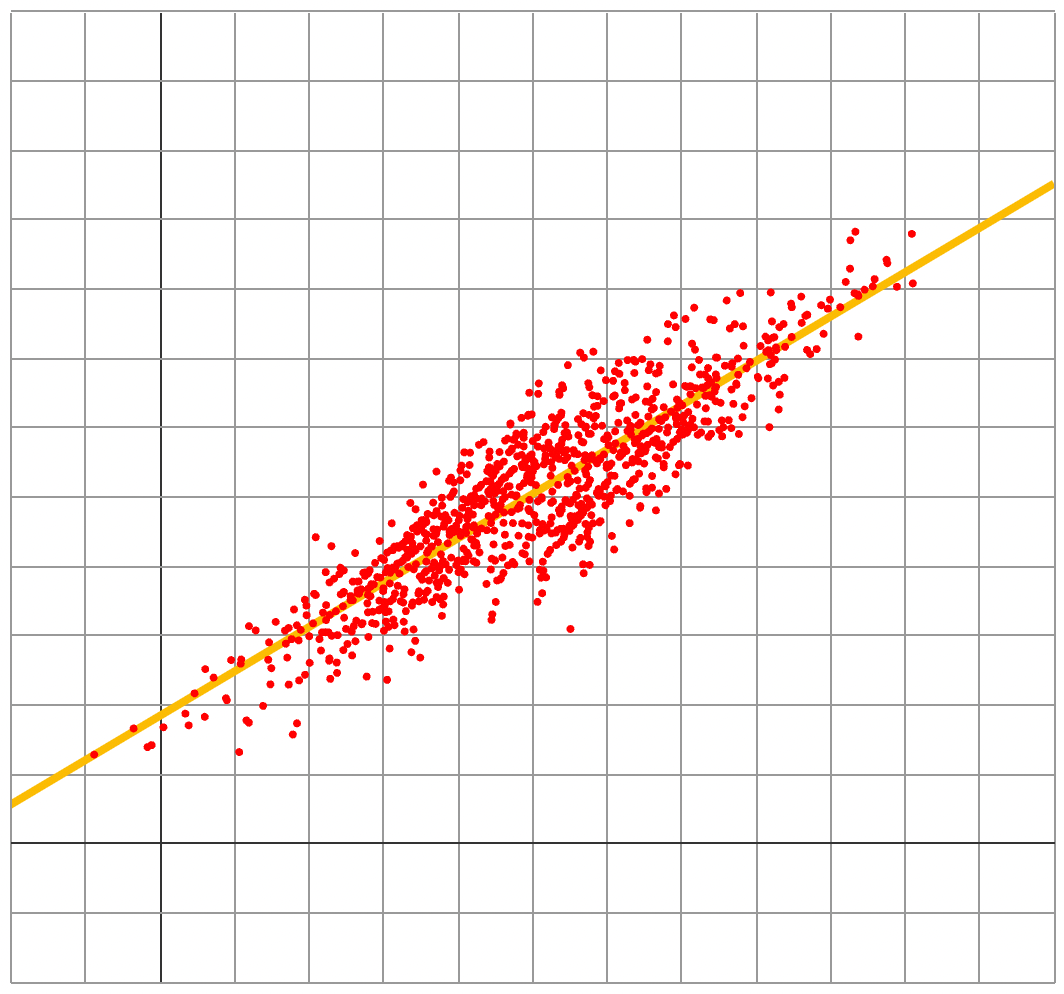
Note that there are no massive outliers at the top of the phenotype distribution.
In other words, the scatterplot doesn’t exhibit any genius phenomenon. It mathematically can’t. In the Gaussian world of highly-heritable polygenic traits, there is no room for Pareto outcomes.
Like most hereditarian fallacies, the genius myth stems from our misguided bias toward deterministic “explanations”, in the face of phenomena whose nature is inherently stochastic.
Bethe’s quote is typical of this deterministic mindset: when he suggests that von Neumann might be “from another species”, he isn’t alluding to 80% heritability, but rather to 99% heritability or more, something akin to genetic determinism: von Neumann had a unique talent because he had a unique genetic make-up.
This contrasts with the above scatterplot, where the “most talented” individual isn’t even the one with the highest polygenic score. Contrary to a common misconception, 80% heritability still is very far from genetic determinism.
But the higher you go with polygenic heritability, the closer you get to a true Gaussian distribution of outcomes, and the harder it gets to account for the extraordinary spread of cognitive talent, the very phenomenon that made you look for a genetic explanation.
In the end, this is a shape mismatch: you can’t fit Terry Tao under a bell curve.
Smells like Yule process
By contrast with Gaussian distributions, Pareto distributions and power laws typically emerge from sequential drawing processes where each step builds on prior results.
The standard mechanism2 is called preferential attachment process, aka Yule process, aka “rich-get-richer” scheme:
start with a given population and hand out $1 to everyone
at each step, randomly allocate an additional dollar to one person in the population, where everyone’s chance to win is proportional to how much they already have,
when repeated indefinitely, this process converges to a Pareto distribution.
Vilfredo Pareto first identified power laws in the context of wealth inequality, but these statistical distributions are ubiquitous in nature and society, whether you model the number of likes on social media posts, the frequency of words and first names, the population of cities, the magnitude of solar flares, or the mass of asteroids. And they always reflect an underlying preferential attachment phenomenon.
Conversely, I don’t know of any quantified trait that follows a Pareto-like distribution and has a well-documented high heritability (say, in the 70%-100% range)—and I’m still waiting for anyone to propose a biologically credible mechanism that yields Pareto-like phenotypes while maintaining high heritability (see the Q&A below for more on this.)
Where do we go from here?
If your prior is that cognitive talent is mostly a matter of genes, it’s unlikely that my argument will 100% convince you. But I do hope that it will help open your eyes.
This is what it did for me.
In my early 20s, I was a struggling pure math PhD student, trapped in a negative feedback loop. I was firmly convinced that I was gifted, but not gifted enough for research-level algebra and geometry, and this was making me quite depressed.
Meanwhile, some of my peers were experiencing unbelievable success dynamics.
The intuition that the two aspects might be connected—the obscene talent gap and the striking feedback mechanisms—prompted me to update my hereditarian priors. It led me to work specifically on rebuilding my self-confidence and place long-term strategic bets on my cognitive development.
When you experience the full journey from struggling PhD student (the cursed way of belonging to the top 0.1%) to proving a conjecture that is older than you (a 0.0001% or 0.00001% event), you acquire a unique perspective on cognitive inequality. To me (and to me only), the simple fact that my position on the math talent ladder changed so much over the years is a compelling proof that this position wasn’t inscribed in my genes.
But I had no way of knowing that at 25.
In retrospect, this intuition that genius isn’t an essence but a state, the outcome of a trajectory, proved foundational to me. It helped me look at the right places and served as a gateway to life-altering insights on how mathematics actually functions, why top mathematicians think in such bizarre ways, and what I could learn from them.
Questions and answers
This post builds on an earlier X thread that went viral and sparked thousands of reactions. I thank everyone who commented on it, enabling me to map out the most frequent questions and objections:
Is this an actual mathematical proof that genius can’t be genetic?
Of course not. It can’t be, since genius isn’t a well-defined notion.
However, it does qualify as a strong heuristic argument, based on solid math. It belongs to the broader category of morphogenetic arguments which, as a mathematician, I tend to find pretty compelling. It reflects how us mathematicians look at the world:
When we see that soap bubbles are round and honeycombs are hexagonal, we think: “OK, these are minimal surfaces.”
When we see elliptic orbits around the Sun, with Kepler laws, we think: “OK, there’s a differential equation that yields that.”
When we see a bell curve, we think: “OK, these are independent coin flips."
And when we see a Pareto distribution, we think: “OK, there’s no way this is caused by genetics.”
Does this contradict the scientific consensus on the heritability of IQ?
Not quite. I’m discussing extreme cognitive talent which, as mentioned above, lies on an open-ended scale that isn’t captured by IQ.
It is important to keep in mind that, while advanced math may feel like a perversely difficult IQ test, this is a massive oversimplification, and there is no reason to assume that the heritability of “math talent”, whatever it means, is strongly tied with that of IQ. As far as I know, there is zero direct evidence supporting the widespread belief that extreme math talent has a genetic origin.
Note also that, at the moment, there is no scientific consensus on a definite figure for the heritability of IQ. Twin models did suggest high figures, based on disputable modeling assumptions (see the next Q&A item below), but direct genomic studies have failed to confirm this and the missing heritability problem is far from resolved.
Alex Young is one of the leading experts on the topic. When I asked him for his gut feel, here’s what he replied:
My sense is that heritability of IQ is in the range of 30-70% with very high confidence.
My argument is entirely compatible with that.
You’re assuming that genome expression is linear, correct?
Correct. The argument that highly heritable highly polygenic traits can only produce Gaussian phenotypes is indeed based on this assumption.
Note however that the vast majority of the heritability literature makes the same exact assumption. It is known to be incorrect, yet it is often considered to be a reasonable first-order simplification when studying large-scale polygenic phenomena.
In particular, linearity is a core modeling assumption of twin studies, essential to their high estimates for the heritability of IQ. If you relax the assumption and update the twin study framework to account for a simple model of pathway-dependent genetic interaction, you end up with much lower figures.
I won’t go into the mathematical details, but my argument is more robust to mild violations of the linearity assumption, as long as these violations remain “local”.3
While real-world genomic expression is never strictly linear, you’d have to come up with a pretty violent nonlinear expression mechanism if you want to produce Pareto-like outcomes. Upon doing that, you will have introduced a massive amount of non-genetic expression noise that will instantly eat away the heritability4 — that is, even before you realize that high-dimensional nonlinear systems are viciously unstable and stochastic chaos at the molecular level is probably incompatible with life.5
What if genius was 99% heritable but in a quasi-Mendelian way, through ultra-high-impact ultra-rare variants?
Why not, on paper. But the counter-argument only works if these variants are powerful enough to break down the Gaussian math of polygenic heritability, and 1/ there is zero evidence for such variants, 2/ you’d observe speciation-like events where “mutant progenitors” would yield “genius dynasties.”
You’re assuming that cognitive talent follows a Pareto distribution, which is questionable.
Correct. However, the argument doesn’t really need talent to follow a Pareto distribution. I framed it this way for the sake of the exposition, but what actually matters is the existence of orders of magnitude differences between individuals, like in my Hugo vs Terry example.
If you agree that there are abysmal gaps in cognitive ability between individuals, then there’s no point nitpicking about the exact shape of the distribution.
If you disagree, then you’re raising a profound and legitimate objection against the very concept of genius. However, this is beyond the scope of the current post, which is specifically concerned with the genius fallacy, the invalid heuristic that abysmal gaps in cognitive ability require abysmal gaps in genetic potential.
Height isn’t a true Gaussian and, in fact, it’s a bit tail-heavy.
Correct. Robert Wadlow, the tallest person in recorded history, was literally too tall to fit under a bell curve: at 2.72m (or, if you prefer, 8’11), he was 14 standard deviations above the mean.
Yet he was only about 60% above the average human height, which brings us back to the prior objection: this isn’t about true Gaussians vs true Pareto distributions, it’s about whether or not near-deterministic genetics can produce orders of magnitude inequalities between individuals of the same species.
An obvious weakness of my poll is that it only offered four options (“60% smarter”, “5x smarter”, “20x smarter”, “on another planet”, as the UX didn’t allow for more choices). In particular, it was missing the “equally smart” and “no opinion” options. I suspect that most people who chose “60% smarter” had implicitly reframed the question in Gaussian IQ terms, which may have biased their vote.
As pointed out by Steve Strogatz, there are alternate mechanisms that also produce Pareto distributions. See Section 4 of this article (here’s the doi.)
In the sense that the non-linearity is concentrated at the level of individual pathways, with each pathway still making a relatively small contribution to the phenotype. By contrast, twin studies estimates aren’t robust to this type of non-linearity.
To illustrate this point, you can have at look at Joseph Bronski’s stress-test of my argument, and my response to it.
This argument might also explains why linear genomics hasn’t become irrelevant, despite the documented existence of gene interactions: life needs homeostatis, which means that epistasis can never get too messy.





"When Usain Bolt set his 9.58 world record in the 100m dash, he ran 1.5% faster than the silver medalist, and only 3% faster than the last-place finisher. Math talent inequality feels radically different from that."
But in sprinting that is huge. His world record is extraordinary. It is 0.11 seconds faster than the 2nd fastest 100m of all time (by Tyson Gay). And to explain how huge that is, to get a 0.11 second gap from Tyson Gay, you have to go down the next 13 fastest men. From Tyson Gay down, it resembles how fastest times normally appear. If you look at other athletics events, you don't see the same pattern with the top 10 athletes. The gaps from top to 2nd are no more than the next 2 or 3.
We could talk about type 2 fibres or Jamaican sprinting but Yohan Blake and Asafa Powell have those. What Blake and Powell don't have is a height of 6'5". And until Bolt, no-one who was 6'5" was a sprinter. 6'2" was as far as it went. 6'5" has disadvantages. But Bolt has been studied. He has one leg shorter than the other (probably from scoliosis), and runs asymetrically and he twists as he runs and it's thought this fixes the problem. He is mostly about this strange combination that is genetic.
Despite your response to this, the answer here is that the genetic effect is non-linear. The fact that standard models of heritability assume linearity is irrelevant. The reason they do that is because nonlinear genetic interactions are too hard to observe: in the sort of data we have access to they are indistinguishable from non-genetic environmental effects. They are also insensitive to selection. But the fact that it’s unrewarding to model them doesn’t mean they don’t exist.
When a talent requires multiple distinct capacities, each of which is heritable via linear and additive genetic factors, but where the facility with the talent is a nonlinear function of the capacities, you can very easily get a pareto distribution. And that seems like a pretty plausible model for math aptitude.
BTW I think that this is compatible with there being a very substantial non-genetic component in mathematical achievement.