The curious case of broken theorems

Mathematics shouldn't survive logical errors—yet it does

Andrew Wiles became an instant superstar on 23 June 1993, when he announced a proof of Fermat’s Last Theorem in front of a packed conference room at the Isaac Newton Institute for Mathematical Sciences in Cambridge. But during the summer, his Princeton colleague Nick Katz spotted a gap in the proof and, by September 1993, it had become clear that there was no easy fix.

Just imagine. You’ve spent the past seven years working secretly on a three-hundred-year-old mathematical problem, one of the hardest in human history. You’re not a ‘fake it till you make it’ grifter. You’re a serious, genuine, respected, high-integrity professional.

How would you react?

It’s hard to imagine all the emotions he must have gone through. But this later interview offers a glimpse. With a teary voice, Wiles recalls the “most important moment of [his] working life”, when he had this “incredible revelation” on 19 September 1994 and finally found a fix.

Wiles did what any experienced mathematician would do in such circumstances: he slept on it.

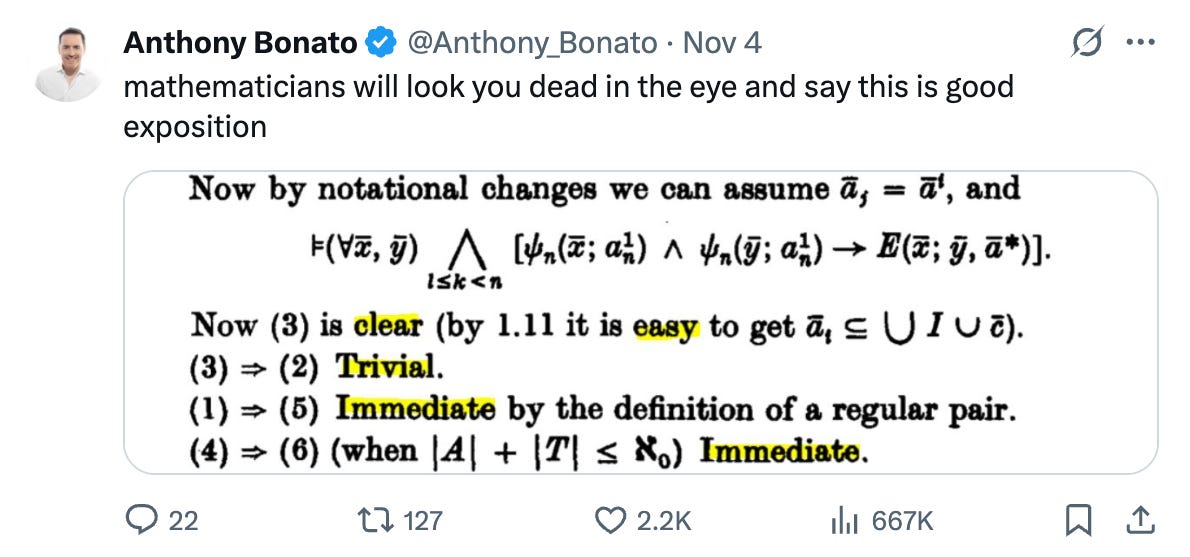
It is a well-known fact, abundantly documented in mathematical folklore, that new proofs have a pretty high mortality rate in the first few days. But Wiles’ “incredible revelation” did survive the night:

I checked through it again the next morning and, by 11 o’clock, I was satisfied. I went down and told my wife: “I’ve got it, I think I’ve got it! I’ve found it!” It was so unexpected, I think she thought I was talking about a children’s toy or something. She said “Got what?” and I said “I’ve fixed my proof, I’ve got it!”

But why, in the first place, is it possible to “fix” a proof? Isn’t a proof supposed to be either valid or invalid? What does it mean for a proof to be broken?

To see the puzzle more clearly, remember that mathematics is supposed to be a logical endeavor and, from a formal logic standpoint, there isn’t much difference between a proof, a computation, or a theorem. A proof is nothing but a peculiar type of theorem—one that asserts that these specific steps constitute a valid logical derivation of statement X.

When rephrased in terms of theorems, the questions become mesmerizing:

Why, in the first place, is it possible to “fix” a theorem? Isn’t a theorem supposed to be either true or false? What does it mean for a theorem to be broken?

Wiles’s example may not feel like a big deal, because his proof was “fixed” long before it was published. But there are instances where broken proofs and broken theorems have slipped into the mathematical corpus and remained there for decades without anyone noticing.

My personal favorite is a 1961 “theorem” in homological algebra that ended up being “disproved” in 2002 article by Amnon Neeman, an Australian mathematician.

Aussie mathematical humor is a niche genre that rarely breaks into the mainstream, but Neeman’s deadpan title has a shot at eternal glory: “A counterexample to a 1961 ‘theorem’ in homological algebra.” The opening paragraph is in the same vein:

Abstract. In 1961, Jan-Erik Roos published a “theorem”, which says that in an [AB4∗] abelian category, lim^1 vanishes on Mittag–Leffler sequences. See Propositions 1 and 5 in [4]. This is a “theorem” that many people since have known and used. In this article, we outline a counterexample.

Now *this* is a pretty big deal, because of a fundamental theorem in formal logic that asserts, basically, that any mathematical theory containing a single contradiction instantly disintegrates into a giant atomic cloud of nonsense, where every statement is both true and false.

According to Google Scholar, Jan-Erik Roos’s 1961 paper was cited 231 times (as of this morning), by articles that have themselves been cited thousands of times, by articles that have themselves been cited a gazillion times, and so forth...

So why is it that Amnon Neeman’s paper didn’t annihilate mathematics?

My take is that this paradox encapsulates a profound aspect of mathematics that has been overlooked for centuries by philosophers and logicians alike and—once properly accounted for—provides a compelling evidence in favor of the dissenting “conceptualist” view on the foundations of mathematics.

Before I articulate the case, let me be clear that this example from homological algebra, albeit extreme, represents a general pattern: published mathematical research is riddled with errors.

My friend Raphaël Rouquier—an outstanding mathematician who was awarded several serious prizes and is a professor at UCLA—maintains an Errata summary that currently references sixteen papers, about 25% of his published research. I am not singling him out because he is sloppy, but because he is ego-less and I know he won’t be offended.

As for the great Terry Tao, he authored four “Erratum” papers correcting four of his earlier works. This is the mathematical equivalent of a security patch—when an error is so significant that a dedicated article must be urgently published to set the record straight.

The mathematical community has been aware of these issues for ages and, in fact, the entire field of mathematics exists as an attempt to get rid of them. This is why proofs were invented. This is why formal logic was invented. This is why research papers are long and tedious. This is why academic journals take ages to get them refereed, accepted, and published.

The current incarnation of this millennial quest is the titanic effort to formalize mathematics, that is, to re-implement existing theorems and proofs within formal “proof assistants” such as Lean. Indeed, while extant mathematics may seem formal to outsiders, this isn’t really the case—it is merely written in a “mock” formal language that mixes abstract symbols with handwaving, and it is a running joke that most proofs are full of gaps. That wouldn’t eliminate the need for human-readable proofs (that cannot span gigabytes), but it would ensure that they are backed by machine-verified formal derivations.

Kevin Buzzard and his team at Imperial College have embarked on a multi-year project to formalize the proof of Fermat’s Last Theorem and, interestingly, they have already been confronted with an “Amnon Neeman moment” of their own.

Kevin reflects on this in a fascinating blog post that goes right to the heart of our topic. Rather than following Wiles’s original reasoning, they adopted a broader approach relying on an abstract machinery called crystalline cohomology, introduced by Alexander Grothendieck and developed in the 1970s by his student Pierre Berthelot.

In the final months of 2024, as Kevin and his team had just set off on this project, they received a message from a French mathematician, Antoine Chambert-Loir, who had noticed some strange behaviors with Lean—it was constantly complaining about the standard human argument behind one key lemma of the theory.

As Antoine later found out, this proof was actually broken. Here’s how Kevin frames it:

According to the way I currently view mathematics (as a formalist), the entire theory of crystalline cohomology vanished from the literature at the moment Antoine discovered the issue, with massive collateral damage (for example huge chunks of Scholze’s work just disappeared, entire books and papers vaporised etc).

But, again, the asteroid ended up not hitting the Earth and not wiping out the dinosaurs: they found a fix!

What is going on here? Why is it never a disaster? What makes mathematicians so incredibly lucky?

Kevin explains it later in his post, revealing along the way that he isn’t a true formalist. True formalism—the technical term is ontological formalism—posits that mathematics is just a meaningless game of meaningless symbols, detached from any semantics humans might project onto it.

For a true formalism, there is no such thing as “fixing” a proof, as the whole edifice shatters into unsalvageable pieces at the exact moment a contradiction is introduced. I have yet to come across a career mathematician who really thinks that.

Kevin is more likely to be a methodological formalist, someone who thinks that computer-aided formalization is the correct framework for implementing mathematical proofs—a position I’m aligned with.

This doesn’t prevent him from attributing meaning to mathematics. In the midst of the crisis, as crystalline cohomology had been cleansed out of formalized mathematics, it continued to exist in Kevin’s brain:

The thing I want to stress is that it was absolutely clear to both me and Antoine that the proofs of the main results were of course going to be fixable, even if an intermediate lemma was false, because crystalline cohomology has been used so much since the 1970s that if there were a problem with it, it would have come to light a long time ago.

This illustrates the plight of the working mathematician, an expression coined by Reuben Hersh and discussed in my earlier piece on conceptualism: the philosophical debate on the foundations of mathematics has been hijacked by an artificial opposition between Platonism and formalism while, in fact, practical mathematics has to borrow from both sides.

Some career mathematicians self-identify as Platonists. Some don’t. But all of them are methodological Platonists, in the sense that no-one can do math without attaching intuitive meaning to the abstract symbols in front of them. You have to actively imagine that the symbols mean something, that they refer to actual “objects”, that these objects do “exist”, somewhere, somehow, in a certain way.

In essence, conceptualism is the synthesis of methodological Platonism with methodological formalism. It posits that mathematics is a human activity that relies on a formal game of “meaningless” logical deduction, as a means of strengthening and solidifying our ability to build new concepts and make intuitive sense of them.

It’s very hard to argue against ontological Platonism, because the only nuance is whether or not these imaginary cognitive objects “really” exist, in the ethereal realm of ideas—which by definition we can’t access.

A pop math trope asserts that ontological formalism was defeated by Kurt Gödel, which I’ve always found unconvincing. Sure, incompleteness was terrible news for Hilbert’s program—but terrible news in itself isn’t supposed to have ontological consequences.

Personally, I only started to view ontological formalism as untenable after I observed the failure modes of mathematics.

Meaningless formal systems should break down like Prince Rupert’s drops, these toughened glass beads that are unbelievably resistant, until you snap them at the right place and they explode into powder.

By contrast, real-world mathematics breaks down like pottery. As a whole, the mathematical corpus is a giant, collaborative work of kintsugi, the Japanese art of pottery-fixing. The whole thing started off as unstructured clay and was made hard by our very hand.

“Fixing” a theorem or a proof isn’t about building entirely new ones. It is about filling small gaps in arguments, or replacing technical lemmas that happen to be false, or replacing a theorem with a similar one that is mildly more restrictive. All these notions—small gaps, technical lemmas, similar theorems with mildly more restrictive conditions—are impossible to make sense of outside of the meaning layer that humans project onto formal systems. Fracture lines don’t propagate too far because they tend to be meaningless. Mathematicians even have a word for this—a statement might be false, yet morally true.

While the formal layer is how mathematics is expressed, the meaning layer is where the real action is taking place—and what holds it together at large scale.